Hašovací funkce, principy, příklady a kolize

Vlastimil Klíma,

http://cryptography.hyperlink.cz/

v.klima@volny.cz

verze 1, 19. 3. 2005

Abstrakt. Příspěvek je určen těm, kdo nemají podrobné znalosti o hašovacích funkcích, ale přitom se jich nějakým způsobem týká jejich bezpečnost. Budeme se zabývat principy konstrukce, bezpečností a novinkami v oblasti hašovacích funkcí.

Obsah

1. Hašovací funkce a jejich vlastnosti 3

1.1. Jednosměrné funkce. 3

1.2. Kryptografická hašovací funkce. 4

1.3. Vstup a výstup. 4

1.4. Jednosměrnost 4

1.5. Odolnost proti kolizi prvního řádu, bezkoliznost prvního řádu. 4

1.6. Odolnost proti kolizi druhého řádu, bezkoliznost druhého řádu. 4

1.7. Častý omyl - nepochopení pojmu bezkoliznost 5

1.8. Orákulum a náhodné orákulum.. 5

1.9. Hašovací funkce jako náhodné orákulum.. 5

1.10. Příklady využití 5

2. Bezpečnost hašovacích funkcí 6

2.1. Bezpečnost z hlediska nalezení vzoru, prolomení hašovací funkce poprvé. 6

2.2. Složitost nalezení kolize. 6

2.3. Tvrzení (narozeninový paradox) 6

2.4. Multikolize. 7

2.5. r-násobná kolize u náhodného orákula. 7

2.6. Bezpečnost z hlediska nalezení kolize, prolomení hašovací funkce podruhé. 7

2.7. Prakticky používané hašovací funkce nejsou prokazatelně bezpečné. 7

2.8. Když je nalezena kolize. 7

2.9. Ilustrace: Útok na MD4. 7

3. Konstrukce moderních hašovacích funkcí 8

3.1. Zarovnání 8

3.2. Damgard-Merklovo zesílení (doplnění o délku původní zprávy) 9

3.3. Damgard-Merklův iterativní princip moderních hašovacích funkcí 9

3.4. Kolize kompresní funkce. 10

3.5. Bezpečnost Damgard-Merklovy konstrukce. 10

3.6. Útok na dlouhé zprávy bez Damgard-Merklova zesílení 11

4. Konstrukce kompresní funkce. 11

4.1. Davies-Meyerova konstrukce kompresní funkce. 11

5. Kompresní a hašovací funkce MD5. 12

5.1. Útok hrubou silou na MD5. 14

5.2. Další útoky na MD5. 14

6. Čínský útok na MD5 (Wangová a kol., 2004) 14

6.1. Hledání čínského triku. 15

6.2. Diferenční schéma. 16

6.3. Další informace o čínském útoku. 17

6.4. Rychlejší metoda nalézání kolizí (Klíma, 2005) 18

6.5. Distribuovaný útok MD5CRACK zastaven. 18

6.6. Využití kolizí - 1. varianta s odlišným počátkem zpráv. 18

6.7. Využití kolizí - 2. varianta s volbou IV a shodným začátkem zpráv. 19

6.8. Co současné útoky na MD5 neumí 20

7. SHA-1 kryptograficky zlomena. 20

8. Některé aplikace, využívající kolize hašovacích funkcí 21

8.1. Příklady využití již publikované čínské kolize MD5. 21

8.2. Jak oklamat certifikační autoritu, používající MD5 nebo SHA-1, aby vydala certifikát na dva různé podpisové klíče. 22

9. Klíčovaný hašový autentizační kód - HMAC.. 23

9.1. Obecná definice HMAC.. 23

9.2. Nepadělatelný integritní kód, autentizace původu dat 25

9.3. Průkaz znalosti při autentizaci entit 25

10. PRF a PRNG a odhad jejich oslabení současnou kryptoanalýzou. 25

10.1. Pseudonáhodná funkce (PRF) při tvorbě klíčů z passwordů (PKCS#5) 25

10.2. Pseudonáhodné generátory (PRNG) 26

10.3. PRNG ve spojení s hašovací funkcí H, PKCS#1 v.2.1. 26

10.4. PRNG ve spojení s hašovací funkcí podle PKCS#5. 27

10.5. PRNG ve spojení s HMAC.. 27

11. Kolize a některá autentizační schémata. 27

12. Třída hašovacích funkcí SHA-2 (SHA-256, 384, 512 a 224) 28

13. Generické problémy iterativních hašovacích funkcí 28

13.1. r-násobná kolize pro iterativní hašovací funkce lze docílit s nižší složitostí 28

13.2. Kaskádovitá konstrukce pozbývá smyslu. 29

13.3. Nalezení druhého vzoru u dlouhých zpráv snadněji než se složitostí 2ⁿ 29

13.4. Závěr k novým zjištěním kryptoanalýzy iterativních hašovacích funkcí. 30

14. NIST plánuje přechod na SHA-2 do r. 2010. 30

15. Závěr: Které techniky jsou a nejsou bezpečné. 30

15.1. Doporučení 30

16. Literatura. 31

1. Hašovací funkce a jejich vlastnosti

Hašovací funkce jsou silným nástrojem moderní kryptologie. Jsou jednou z klíčových kryptologických myšlenek počítačové revoluce a přinesly řadu nových použití. V jejich základu jsou pojmy jednosměrnosti (synonymum: jednocestnost) a bezkoliznosti.

1.1. Jednosměrné funkce

Jsou to takové funkce f: X ® Y, pro něž je snadné z jakékoli hodnoty x Î X vypočítat y = f(x), ale pro nějaký náhodně vybraný obraz y Î f(X) nelze (je to pro nás výpočetně nemožné) najít její vzor x Î X tak, aby y = f(x).

Přitom víme, že takový vzor existuje nebo jich existuje dokonce velmi mnoho.

Příklad:

vynásobení dvou velkých prvočísel, v současné době neznáme dostatečně rychlou metodu jak tato čísla separovat

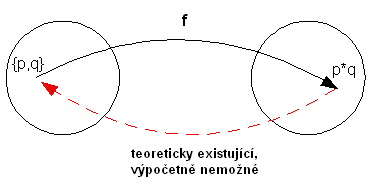
Obr.: Jednosměrná funkce

Druhou odnoží jednosměrných funkcí jsou jednosměrné funkce s padacími vrátky. Bývají také nazývány jednosměrné funkce se zadními vrátky, pokud je zřejmé, že se nejedná o pirátská vrátka do systému. Je na nich založena asymetrická kryptografie.

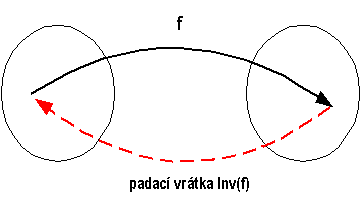
Obr.: Jednosměrné funkce s padacími vrátky

Hašovací funkce jsou jednosměrné funkce bez padacích vrátek.

1.2. Kryptografická hašovací funkce

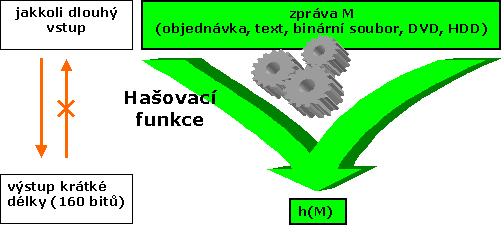
Hašovací funkce byla původně označením pro funkci, která libovolně velkému vstupu přiřazovala krátký hašovací kód o pevně definované délce.

Nyní se pojem hašovací funkce používá v kryptografii pro kryptografickou hašovací funkci, která má oproti původní definici ještě navíc vlastnost jednosměrnosti a bezkoliznosti.

1.3. Vstup a výstup

Hašovací funkce h zpracovává prakticky neomezeně dlouhá vstupní data M na krátký výstupní hašový kód h(M). Například u hašovacích funkcí MD5/SHA-1/SHA-256/SHA-512 je to 128/160/256/512 bitů.

1.4. Jednosměrnost

Hašovací funkce musí být jednosměrná (one-way) a bezkolizní (collission-free). Jednosměrnost znamená, že z M lze jednoduše vypočítat h(M), ale obráceně to pro náhodně zadaný hašový kód H je výpočetně nezvládnutelné.

1.5. Odolnost proti kolizi prvního řádu, bezkoliznost prvního řádu

Bezkoliznost (stručnější označení pro "odolnost proti kolizi") požaduje, aby bylo výpočetně nezvládnutelné nalezení libovolných dvou různých (byť naprosto nesmyslných) zpráv M a M´ tak, že h(M) = h(M´). Pokud se toto stane, říkáme, že jsme nalezli kolizi. Bezkoliznosti, kterou jsme právě popsali, říkáme bezkoliznost 1. řádu nebo jednoduše bezkoliznost.

Bezkoliznost se, jak jsme uvedli, zásadním způsobem využívá k digitálním podpisům. Nepodepisuje se přímo zpráva, často velmi dlouhá (u MD5/SHA-1/SHA-256 prakticky až do délky D = 2⁶⁴-1 bitů), ale pouze její haš. Můžeme si to dovolit, protože bezkoliznost zaručuje, že není možné nalézt dva dokumenty se stejnou haší. Proto můžeme podepisovat haš.

1.6. Odolnost proti kolizi druhého řádu, bezkoliznost druhého řádu

Další nejznámější definice je odolnost proti nalezení druhého vzoru neboli bezkoliznost druhého řádu. Řekneme, že hašovací funkce h je odolná proti nalezení druhého vzoru, jestliže pro daný náhodný vzor x je výpočetně nezvládnutelné nalézt druhý vzor y ¹ x tak, že h(x) = h(y).

1.7. Častý omyl - nepochopení pojmu bezkoliznost

Možných zpráv je mnoho (1 + 2¹ + ... + 2^D = 2^D+1 -1) a hašovacích kódů málo (u MD5 například pouze 2¹²⁸). Musí proto existovat ohromné množství zpráv, vedoucích na tentýž hašový kód - v průměru je to řádově 2^D-127. Kolizí tedy existuje ohromné množství. Pointa je v tom, že nalezení byť jediné kolize je nad naše výpočetní možnosti.

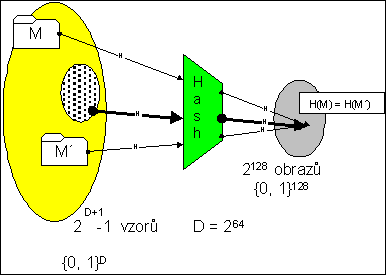
Obr. : Kolize

1.8. Orákulum a náhodné orákulum

Orákulum nazýváme libovolný stroj (stroj "podivuhodných vlastností"), který na základě vstupu odpovídá nějakým výstupem. Má pouze vlastnost, že na tentýž vstup odpovídá tímtéž výstupem. Náhodné orákulum je orákulum, které na nový vstup odpovídá náhodným výběrem výstupu z množiny možných výstupů.

1.9. Hašovací funkce jako náhodné orákulum

Z hlediska bezpečnosti bychom byli rádi, kdyby se hašovací funkce chovala jako náhodné orákulum. Odtud se odvozují bezpečnostní vlastnosti.

1.10. Příklady využití

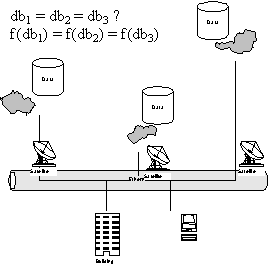
Obr.: Kontrola shodnosti vzdálených rozsáhlých databází

Příklady

• kontrola integrity (kontrola shodnosti velkých souborů dat)
• automatické dešifrování (souboru, disku apod.)
• ukládání a kontrola přihlašovacích hesel
• prokazování autorství
• jednoznačná identifikace dat (jednoznačná reprezentace vzoru, digitální otisk dat, jednoznačný identifikátor dat, to vše zejména pro digitální podpisy)
• prokazování znalosti
• autentizace původu dat
• nepadělatelná kontrola integrity
• pseudonáhodné generátory, derivace klíčů

2. Bezpečnost hašovacích funkcí

2.1. Bezpečnost z hlediska nalezení vzoru, prolomení hašovací funkce poprvé

Pokud se bude hašovací funkce f: {0,1}^D ® {0,1}ⁿ chovat jako náhodné orákulum, bude složitost nalezení vzoru k danému hašovacímu kódu rovna 2ⁿ.

Pokud je nalezena cesta, jak vzory nalézat jednodušeji, hovoříme o prolomení hašovací funkce.

2.2. Složitost nalezení kolize

Jestliže kolize zákonitě existují, položme si otázku, jak velká musí být množina náhodných zpráv, aby v ní s nezanedbatelnou pravděpodobností existovaly dvě různé zprávy se stejnou haší. Narozeninový paradox říká, že pro n-bitovou hašovací funkci nastává kolize s cca 50% pravděpodobností v množině 2^n/2 zpráv, namísto očekávaných 1/2 * 2ⁿ. Například pro 160bitový hašový kód bychom očekávali 1/2 *2¹⁶⁰ zpráv, paradoxně je to pouhých 2⁸⁰ zpráv.

2.3. Tvrzení (narozeninový paradox)

Mějme množinu M m různých koulí a proveďme výběr k koulí po jedné s vracením do množiny M. Potom pravděpodobnost, že vybereme některou kouli dvakrát nebo vícekrát je P(m, k) = 1 - m(m -1)...(m - k + 1)/m ^k. Pro k = O(m ^1/2) a m velké je P(m, k) » 1 - exp(-k²/2m).

Důsledek

Pro m velké se ve výběru k = (2m * ln_e2)^1/2 » m^1/2 prvků z M s cca 50% pravděpodobností naleznou dva prvky shodné.

Paradoxnost.

Běžně by člověk uvažoval následovně. Máme množinu m prvků, vezmeme si jeden prvek a hledáme k němu druhý. Abychom dostali pravděpodobnost 1/2, musíme vytahat asi polovinu množiny M, tj. m/2 prvků. Místo toho ale postačí odmocnina z m prvků.

Máme P(365, 23) = 0.507. Pro čísla m = 365 a k = 23 interpretujeme tvrzení tak, že skupina 23 náhodně vybraných lidí postačí k tomu, aby se mezi nimi s cca 50% pravděpodobností našla dvojice, slavící narozeniny tentýž den. U skupiny 30 lidí je pravděpodobnost už P(365, 30)= 0.706.

Tvrzení se zdá paradoxní protože, ač je vyřčeno jinak, obvykle ho vnímáme ve smyslu "kolik lidí je potřeba, aby se k danému člověku našel jiný, slavící narozeniny ve stejný den". V této podbízející se interpretaci hledáme jedny konkrétní narozeniny, nikoli "jakékoliv shodné" narozeniny. Oba přístupy odráží přesně rozdíl mezi kolizí prvního řádu (libovolní dva lidé) a druhého řádu (nalezení druhého člověka k danému).

2.4. Multikolize

Multikolizí (r-násobnou kolizí, r-cestnou kolizí) nazýváme r-tici různých zpráv, vedoucích na stejnou haš.

2.5. r-násobná kolize u náhodného orákula

K tomu, abychom mezi odpověďmi náhodného orákula na N různých dotazů nalezli jednu odpověď r krát (r-násobnou kolizi), postačí s dostatečnou nenulovou pravděpodobností N = 2^{n*(r - 1) /r} dotazů, což je pro větší r přibližně 2ⁿ. Pro r = 2 dostáváme známý narozeninový paradox a složitost 2^n/2. Pojmem r-násobné kolize se poprvé zabýval Merkle na konferenci Crypto 1989.

2.6. Bezpečnost z hlediska nalezení kolize, prolomení hašovací funkce podruhé

Pokud se hašovací funkce f: {0,1}^D ® {0,1}ⁿ bude chovat jako náhodné orákulum, bude složitost nalezení kolize rovna přibližně 2^n/2.

Pokud je nalezena cesta, jak kolize nalézat jednodušeji, hovoříme o prolomení hašovací funkce.

2.7. Prakticky používané hašovací funkce nejsou prokazatelně bezpečné

I když uvidíme, že vytváření hašovacích kódů je opravdu neskutečně složité, nalezení kolizí je přesto pouze otázkou intelektuální výzvy, neboť u prakticky používaných hašovacích funkcí není prokázána výpočetní složitost nalezení kolize nebo druhého vzoru. Jejich bezpečnost tak u obou vlastností (jednosměrnost, bezkoliznost) závisí pouze na stavu vědy v oblasti kryptografie a kryptoanalýzy.

Prolomení některých kryptografických technik je proto přirozeným a průvodním jevem rozvoje poznání v této oblasti.

2.8. Když je nalezena kolize

Hašovací funkce, u níž byla nalezena kolize, ztrácí generálně smysl, neboť hypotéza o tom, že se chová jako náhodné orákulum byla vyvrácena. Zejména by neměla být používána k digitálním podpisům, neboť tam kolize znamená, že je možné předložit dvě různé zprávy s tímtéž platným digitálním podpisem, platným pro obě zprávy. Existují ale techniky, kde nejsou využity všechny vlastnosti hašovací funkce a kde porušení bezkoliznosti (nebo částečné porušení bezkoliznosti) nevadí (PRNG, PRF, HMAC).

2.9. Ilustrace: Útok na MD4

U MD4 předložil v roce 1996 H. Dobbertin na konferenci FSE 1996 metodu nalézání kolizí a velmi instruktivní kolizi hašovací funkce [D96a], viz obrázek.

Obr.: Kolize u MD4 [D96a]

3. Konstrukce moderních hašovacích funkcí

U moderních hašovacích funkcí může být zpráva velmi dlouhá, například D = 2⁶⁴-1 bitů. Je zřejmé, že takovou zprávu musíme zpracovávat po částech, nikoli najednou. Také v komunikacích je přirozené, že zprávu dostáváme po částech a nemůžeme ji z paměťových důvodů ukládat celou pro jednorázové zhašování.

Odtud vyplývá nutnost hašování zprávy po blocích a sekvenční způsob.

Ze zpracování po blocích plyne také nutnost zarovnání vstupní zprávy na celistvý počet bloků před hašováním.

Předpokládejme, že máme hašovací funkci o n-bitovém hašovacím kódu a zprávu M zarovnanou na m-bitové bloky m₁,..., m_N.

3.1. Zarovnání

Zarovnání musí být takové, aby umožňovalo jednoznačné odejmutí, jinak by vznikaly jednoduché kolize. Například při doplnění zprávy nulovými bity by nešlo rozeznat, kolik jich bylo doplněno, a zda některé z nich nejsou platnými bity zprávy, pokud by zpráva nulovými bity končila.

Například doplněná zpráva

10111100110101000000000000000000000000000

by byla doplněním zpráv

10111100110101

101111001101010

1011110011010100

10111100110101000

...

10111100110101000000000000000000000000000,

a všechny by proto vedly ke kolizi (měly by stejný hašový kód), dokonce multiplikativní kolizi.

Zarovnání u moderních hašovacích funkcí se definuje jako doplnění bitem 1 a poté potřebným počtem bitů 0. To umožňuje jednoznačné odejmutí doplňku.

3.2. Damgard-Merklovo zesílení (doplnění o délku původní zprávy)

Za potřebným počtem bitů je ještě nutné doplnit délku původní zprávy, jinak by bylo možné vést útok, popsaný dále. Tomuto doplnění se říká Damgard-Merklovo zesílení, které bylo nezávisle oběma autory navrženo na konferenci Crypto 1989. Doplnění ilustruje obrázek (viz dále) pro blok délky m = 512, který je použit u hašovacích funkcí MD4, MD5, SHA-0, SHA-1, SHA-256.

Doplnění se provádí tak, že M je nejprve doplněna bitem 1, poté co nejmenším počtem nulových bitů (může jich být 0 - 447) tak, aby do celistvého násobku 512 bitů zbývalo ještě 64 bitů, a nakonec je těchto 64 bitů vyplněno 64bitovým vyjádřením počtu bitů původní zprávy M. Délka zprávy tedy také vstupuje do hašovacího procesu. Rezervace 64 bitů na délku zprávy umožňuje hašovat zprávy až do délky D = 2⁶⁴-1 bitů.

3.3. Damgard-Merklův iterativní princip moderních hašovacích funkcí

Všechny současné prakticky používané hašovací funkce používají Damgard-Merklův (DM) princip iterativní hašovací funkce s využitím kompresní funkce.

Vstupy kompresní funkce

Kompresní funkce f zpracovává aktuální blok zprávy m_i. Výsledkem je určitá hodnota, které se říká kontext a označuje H_i. Hodnota kontextu pak nutně tvoří vstup do kompresní funkce v dalším kroku. Kompresní funkce má tedy dva vstupy - kontext a aktuální blok zprávy. Výstupem je nový kontext.

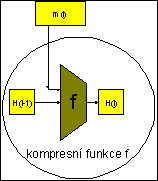
Damgard-Merklova konstrukce

Odtud vznikla iterativní konstrukce, popsaná vzorcem

H_i = f (H_i-1, m_i),

H₀ = IV,

která se nazývá Damgard-Merklova metoda (resp. Merklova meta metoda), neboť ji oba dva nezávisle navrhli na konferenci Crypto 1989.

Hašování probíhá postupně po jednotlivých blocích m_i v cyklu podle i od 1 do N. Kompresní funkce f v i-tém kroku (i = 1,..., N) zpracuje vždy daný kontext H_i-1 a blok zprávy m_i na nový kontext H_i. Šíře kontextu je většinou stejná jako šíře výstupního kódu.

Počáteční hodnota kontextu H₀ se nazývá inicializační hodnota (IV). Je dodefinována jako konstanta daná v popisu každé iterativní hašovací funkce.

Vidíme, že název kompresní funkce je vhodný, neboť funkce f zpracovává širší vstup (H_i-1, m_i) na mnohem kratší H_i, tedy blok zprávy m_i se sice funkčně promítne do H_i, ale současně dochází ke ztrátě informace (šířka kontextu H₀, H₁,...H_i,... zůstává stále stejná). Kontextem bývá obvykle několik 16bitových nebo 32bitových slov, u MD5 jsou to čtyři slova A, B, C, D (dohromady 128 bitů).

Po zhašování posledního bloku m_N dostáváme kontext H_N, z něhož bereme buď celou délku nebo část jako výslednou haš. U funkce MD5 je šířka kontextu 128 bitů a výslednou haš tvoří všech 128 bitů kontextu H_N.

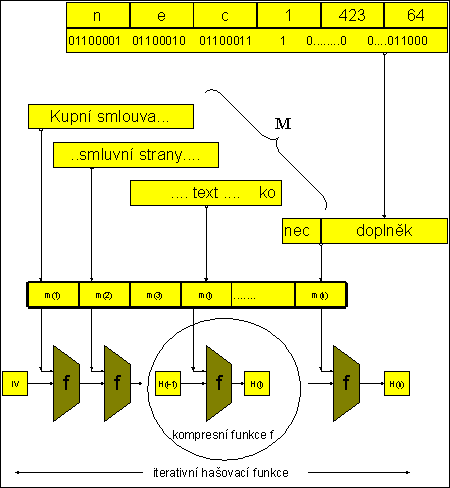
Obr.: Doplňování, kompresní funkce a iterativní hašovací funkce

3.4. Kolize kompresní funkce

Kolize kompresní funkce f spočívá v nalezení inicializační hodnoty H a dvou různých bloků B₁ a B₂ tak, že f(H, B₁) = f(H, B₂).

3.5. Bezpečnost Damgard-Merklovy konstrukce

Pokud je hašovací funkce bezkolizní, vyplývá odtud i bezkoliznost kompresní funkce. (Důkaz je triviální pro zprávu tvořící jeden blok.) Je-li kompresní funkce bezkolizní, obecně odtud nevyplývá, že je bezkolizní i hašovací funkce.

Avšak u Damgard-Merklovy konstrukce to bylo dokázáno. Tj. pokud je kompresní funkce bezkolizní, je bezkolizní také iterovaná hašovací funkce, konstruovaná z ní výše uvedeným postupem.

Tato vlastnost Damgard-Merklovy konstrukce je bezpečnostním základem všech moderních hašovacích funkcí.

Tím pádem bylo možné se soustředit na nalezení kvalitní kompresní funkce.

3.6. Útok na dlouhé zprávy bez Damgard-Merklova zesílení

Pokud bychom zprávu M doplňovali jen bitem 1 a nulovými bity do nejbližšího celistvého bloku a nepoužili doplnění o délku zprávy, pak bychom mohli najít druhý vzor M´ tak, že h(M´) = h(M) se složitostí menší než 2ⁿ operací (Winternitz, 1984).

Postup.

• Máme dánu zprávu M a hledáme druhý vzor pro hašovací hodnotu h(M).
• Při hašování zprávy M = m₁, m₂, ..., m_N si zaznamenáme všechny průběžné kontexty h_i.
• Vygenerujeme si K = 2ⁿ/N náhodných bloků B_j a vytvoříme seznam kontextů h´_j = f(IV, B_j), j = 1, ..., K.
• V množinách {h_i}_i a {h´_j}_j nalezneme kolizi, tj. takové i a j, že h_i = h´_j. Z binomické věty vyplývá, že střední hodnota počtu nalezených kolizí je pro K = 2ⁿ / N rovna 1 - (1 - N/2ⁿ)^K = NK/2ⁿ » 1.
• Zprávy (m₁, m₂, ..., m_i, m_i+1, ..., m_N), a (B_j, m_i+1, ..., m_N) mají stejnou haš h(M).
• Složitost tohoto postupu je K + N = K = 2ⁿ/N + N, což zejména pro dlouhé zprávy je řádově menší než 2ⁿ.

4. Konstrukce kompresní funkce

Kompresní funkce musí být velmi robustní, aby zajistila dokonalé promíchání bitů zprávy a jednocestnost.

Jak tyto funkce konstruovat? Protože hašovací funkce musí být jednocestné a chovat se co nejvíce jako náhodné orákulum, máme možnost je konstruovat na bázi známých jednocestných funkcí. Můžeme použít znalostí z oblasti blokových šifer. Kvalitní bloková šifra E_k(x) se při pevném klíči k také má chovat jako náhodné orákulum. Dále zaručuje, že známe-li jakoukoli množinu vstupů-výstupů, tj. otevřených-šifrových textů (x, y), nemůžeme odtud určit (díky složitosti) klíč k. Vzhledem ke klíči je tak bloková šifra jednocestná. Přesněji pro každé x je funkce k ® E_k(x) jednocestná. Odtud vyplývá možnost konstrukce kompresní funkce takto:

H_i = E_mi(H_i-1),

kde E je kvalitní bloková šifra.

Vezměme hašování krátké zprávy, která i se zarovnáním tvoří jediný blok zprávy. Máme H₁ = E_m1(IV). Je vidět, že z hodnoty hašového kódu H₁ nejsme schopni určit m₁, čili máme zaručenu vlastnost jednocestnosti.

4.1. Davies-Meyerova konstrukce kompresní funkce

Davies-Meyerova konstrukce kompresní funkce pak zesiluje vlastnost jednocestnosti ještě přičtením vzoru před výstupem:

H_i = f(H_i-1, m_i) = E_mi(H_i-1) xor H_i-1.

Výstup je zde tedy navíc maskován vstupem, což ještě více ztěžuje případný zpětný chod. Protože blok zprávy m_i je obvykle velmi velký (512 bitů) a klíče blokových šifer tak dlouhé nebývají, aplikuje se bloková šifra několikrát za sebou (v rundách), přičemž (rundovní) klíč postupně čerpá z bloku m_i. Na schématu MD5 vidíme jak blokovou šifru, tak způsob, jakým je blok zprávy m_i v 16 rundách po částech používán jako rundovní klíč. Navíc se tento stavební blok ještě čtyřikrát opakuje, takže každá část bloku m_i se projeví na místě klíče dokonce čtyřikrát. Této fázi se proto někdy paradoxně říká příprava klíče, i když se jedná o přípravu zprávy.

5. Kompresní a hašovací funkce MD5

U MD5 tvoří kontext 4 32bitová slova A, B, C a D. Na obrázku vidíme zvětšenu jednu rundu hašování. m_i je jeden 512 bitový blok zprávy. Ten je rozdělen na 16 32bitových slov M₀, M₁, ..., M₁₅, a tato posloupnost je opakována 4x za sebou (v různých permutacích). Na obrázku vidíme, že v kompresní funkci se kontext "zašifruje" vždy jedním 32bitovým slovem M_i. Poznamenejme, že na místě dílčí funkce F v obrázku se po 16 rundách střídají 4 různé (nelineární i lineární) funkce (F, G, H, I) a v každé rundě se využívá jiná konstanta K_i. Po 64 rundách dojde ještě k přičtení původního kontextu (H_i-1) k výsledku podle Davies-Meyerovy konstrukce (xor je nahrazen aritmetickým součtem modulo 2³²). Tak vznikne nový kontext H_i. Pokud by zpráva M měla jen jeden blok, byl by kontext (A, B, C, D) celkovým výsledkem. Pokud ne, pokračuje se stejným způsobem v hašování druhého bloku zprávy m₂ jakoby s inicializační hodnotou H_i-1. Po zpracování bloku m_N máme v registrech výslednou 128bitovou haš H_N.

Pozn.: V obrázku značí plus ve čtverečku modulární součet a výraz x <<< s označuje cyklický posun 32bitového slova x o s bitů doleva.

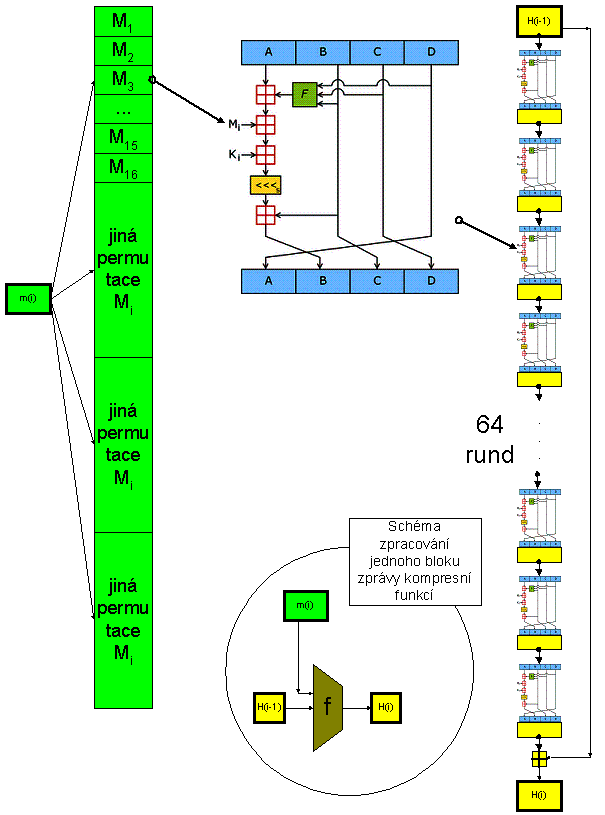
Obr.: MD5

5.1. Útok hrubou silou na MD5

V roce 1994 navrhli P. van Oorschot a M. Wiener paralelně pracující stroj na vyhledávání kolizí za cenu 10 milionů dolarů [OOW94]. Během 24 dnů by uměl vyhledat kolizi.

5.2. Další útoky na MD5

V roce 1993 dvojice Boer-Bosselaers [BoBo93] na konferenci Eurocrypt 1993 ukázala pseudokolizi kompresní funkce MD5. Nalezli H, H´ a X tak, že f(H, X) = f(H´, X).

V roce 1996 na rump session konference Eurocrypt 1996 H. Dobbertin ( [DO96eu] , viz též [DO96cb]) prezentoval kolizi kompresní funkce MD5. Nalezl H, X a X´tak, že f(H, X) = f(H, X´).

6. Čínský útok na MD5 (Wangová a kol., 2004)

V srpnu 2004 byly na rump session konference Crypto 2004 prezentovány kolize hašovacích funkcí MD4, MD5, HAVAL-128 a RIPEMD [WFLY04]. Budeme se věnovat pouze MD5. Číňané přišli s metodou, jak nalézt kolize dvou různých 1024bitových zpráv. Spočívá v tom, že nejprve naleznou dvě různé 512bitové půlzprávy (bloky) M1, M2, což jim trvá cca hodinu na velkém 32procesorovém počítači IBM p690, a potom k nim naleznou dvě různé 512bitové půlzprávy N1, N2 (což trvá už jen sekundy) tak, že složené zprávy (M1, N1) a (M2, N2) mají stejnou haš.

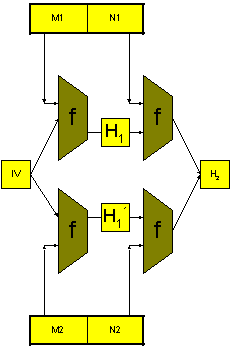
Obr.: Princip čínského útoku na MD5

Uvádí předpis, jak se mají lišit první poloviny M1 a M2 a druhé poloviny N1 a N2. Konkrétně M2 = M1 + C, N2 = N1 - C, kde C je vhodná 512bitová konstanta, mající v binárním vyjádření pouze 3 bity nenulové. Hlavní myšlenkou útoku tedy bylo najít takovou zvláštní konstantu C a pak během první hodiny útoku nalézt zprávu M1 tak, aby M1 a M2 = M1 + C při hašování vedly na různé kontexty H₁ a H₁´ (viz obrázek) takové, že tato odlišnost je srovnána při hašování následných bloků N1 a N2, tj. kontexty H₂ jsou už totožné. Protože zprávy jsou 1024bitové, jsou doplněny ještě dalším blokem (viz definice doplňování) 10..........0 0...10000000000, který je ale pro obě zprávy stejný, neboť mají stejné délky 1024 bitů, takže i kontext H₃ (výsledná haš) je stejný.

Uvedená vlastnost však neplatí pro všechny bloky M1, N1 a všechny konstanty C, takže je nutné je zvláštním způsobem konstruovat. To tvořilo neznámé know-how čínského týmu.

6.1. Hledání čínského triku

V říjnu 2004 se australský tým pokusil čínskou metodu zrekonstruovat pouze na základě zveřejněných kolizí [HPR04]. Nejdůležitější "čínský trik" se nepodařilo objevit, ale na základě dat z [WFLY04] bylo dobře popsáno diferenční schéma, kterým uveřejněné čínské kolize vyhovují. Naplnění podmínek tohoto schématu bylo však ještě příliš náročné a výpočetně složitější, než ukazovaly výsledky z [WFLY04], a tak práce nepřinesla čistě praktické výsledky.

6.2. Diferenční schéma

Z časových a prostorových důvodů zde uvádíme pouze ilustraci pro potřebu přednášky.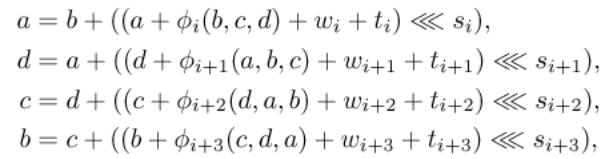

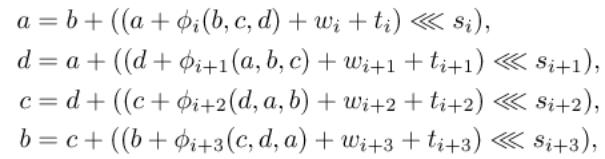
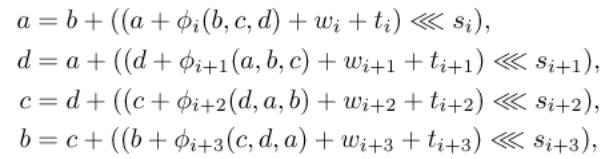
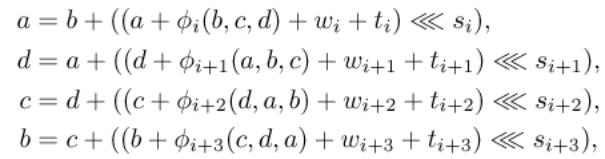
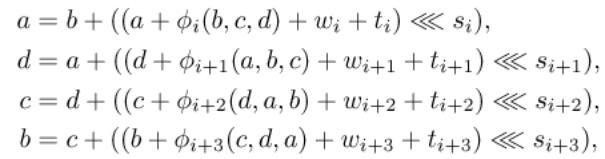
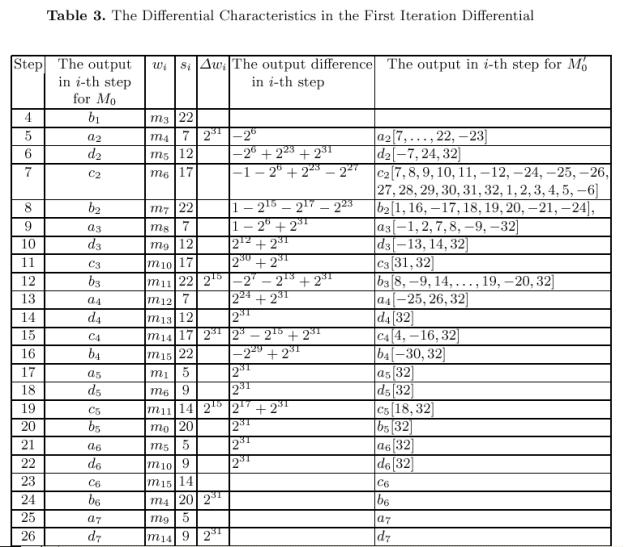
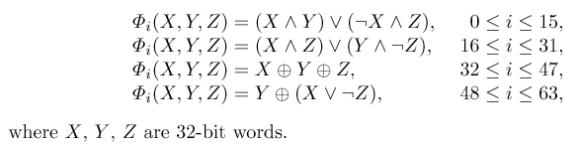
Obr.: Část diferenčního schématu z [WY2005]

Obr.: Použité nelineární a lineární funkce

6.3. Další informace o čínském útoku

V březnu 2005 byla předběžně publikována práce [WY2005], která bude prezentována v květnu na konferenci Eurocrypt 2005.

Prezentuje dvě základní myšlenky útoku, a to diferenční schéma a tzv. metoda modifikace zpráv. Jak diferenční schéma funguje, bylo v zásadě prozkoumáno australským týmem v říjnu 2004 [HPR04] . Čínské diferenční schéma se liší v několika překvapivých detailech, ale jak bylo vytvořeno, zůstává stále utajeno. Pouze je poznamenáno, že vzniklo tak, aby bylo výhodné pro pozdější fáze schématu. U metody modifikace zpráv je uveden jeden příklad s tím, že se dále uvádí, že k hledání jsou použity i jiné modifikace zpráv. Podrobnosti této metody tedy zůstávají i nadále utajeny.

6.4. Rychlejší metoda nalézání kolizí (Klíma, 2005)

Na počátku března 2005 byla také publikována zpráva [VK2005], z níž vyplývá možnost generovat kolize MD5 na domácím počítači, pro libovolnou inicializační hodnotu a rychleji, než prezentoval čínský tým. Metoda také není publikována, pouze je známo, že používá dvoufázový postup jako v [WFLY04] s tím, že v první fázi je 1000 - 2000 krát rychlejší a v druhé 2 - 80 krát pomalejší (celkově 3 - 6 krát rychlejší). Průměrná doba nalezení kolize touto metodou na notebooku (Pentium 1.6 GHz) činí 8 hodin.

Po publikování [WY2005] se potvrdilo, že oba přístupy jsou nikoli diametrálně, ale přesto odlišné.

6.5. Distribuovaný útok MD5CRACK zastaven

O nalezení kolizí MD5 hrubou silou se pokoušel i projekt MD5CRACK na http://www.md5crk.com/, kde Češi patřili k významným přispěvatelům strojového času. Cílem bylo přesvědčit bezpečnostní architekty, aby od MD5 konečně ustoupili. Jakmile byl publikován čínský výsledek, projekt byl pochopitelně zastaven.

Od doby spuštění neuplynulo tolik času, ale pokrok je významný, vzhledem k tomu, že kolizi může vygenerovat jeden člověk na notebooku. Pochopitelně, že takové otázky vyvstávají i pro SHA-1.

6.6. Využití kolizí - 1. varianta s odlišným počátkem zpráv

Hlavní myšlenka tedy je, že první odlišné bloky zpráv vytvoří sice různé kontexty H₁ a H₁´, ale druhé bloky to srovnají na celkový stejný výsledek H₂. Pokud nyní hašování buď ukončíme nebo budeme v obou případech pokračovat už jen stejnými bloky zprávy, obdržíme v obou případech stejný kontext H₃, H₄,..., tedy kolizi. Proto za bloky (M1, N1) a (M2, N2) můžeme připojit libovolnou společnou zprávu T, což povede na stejnou haš.

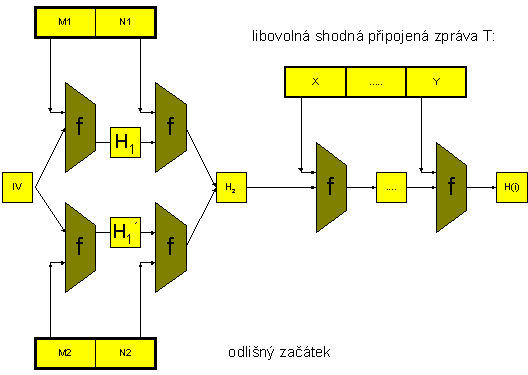
Obr.: Rozšiřování kolizí připojením libovolné zprávy

6.7. Využití kolizí - 2. varianta s volbou IV a shodným začátkem zpráv

Obě práce [WFLY04] i [VK2005] umí nalézt kolize pro libovolnou inicializační hodnotu IV, nejen tu, která je pevně definována pro MD5.

Můžeme proto zvolit libovolnou smysluplnou zprávu T a poté k ní konstruovat (M1, N1) a (M2, N2) tak, že h(T, M1, N1) = h(T, M2, N2), čili zahajovat kolidující zprávy libovolnou zvolenou zprávou. Proč? Když hašujeme zprávu (T, .....) dojdeme po zhašování T (uvažujeme T zarovnanou na bloky) k určitému kontextu H_n. Ten prohlásíme za novou inicializační hodnotu H₀^’ a pro ni nalezneme kolizi (M1, N1) a (M2, N2). Takže platí, že h(T, M1, N1) = h(T, M2, N2) pro libovolnou zprávu T zarovnanou na bloky.

Připojíme-li předchozí výsledek, vedou na stejnou haš i zprávy (T, M1, N1, W) a (T, M2, N2, W) pro libovolné T a W, jak ukazuje obrázek. To lze dále rozvíjet například takto:

(X, M1, N1, Y, O1, P1, Z, Q1, R1, T), (Soubor 1)

(X, M2, N2, Y, O2, P2, Z, Q2, R2, T) (Soubor 2)

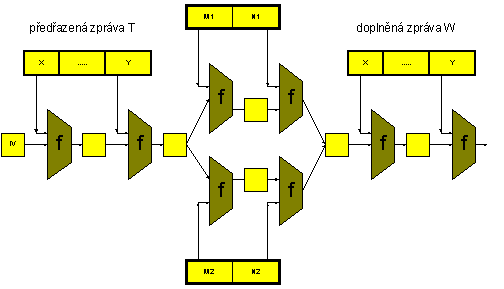
Obr.: Rozšiřování kolidujících zpráv na obě strany

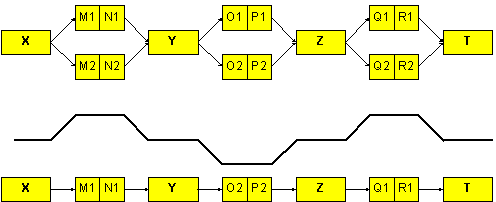
Obr.: Kombinace kolizí a doplňků

6.8. Co současné útoky na MD5 neumí

Neumíme k danému dokumentu nalézt jiný, se stejnou haší! Umíme pouze najít dva různé dokumenty (soubory) se stejnou haší. Útočník navíc musí obě kolidující zprávy vytvářet sám.

V karikatuře si můžeme představit například jak zaměstnanec dává nadřízenému podepsat žádost o dovolenou, se kterou mu „náhodou“ koliduje příkaz na zvýšení platu.

Je to přesně rozdíl mezi kolizemi 1. a 2. řádu. Umíme nalézt kolize 1. řádu, ale ne 2. řádu.

7. SHA-1 kryptograficky zlomena

Tým Wangové vydal 13. 2. 2005 zprávu [WYY05], v níž ukazují plnou kolizi SHA-0 a kolizi SHA-1 pro 58 kroků (z 80). Oznamují též, že jsou schopni nalézt kolizi plnohodnotné SHA-1 se složitostí 2⁶⁹ hašovacích operací. SHA-0 by pokořili se složitostí 2³³ hašovacích operací. Pokud si uvědomíme, že SHA-0 byla určitou dobu standardem, a že se liší od SHA-1 pouze v jedné operaci v základní smyčce, je to ohromný výsledek. Pokud by SHA-1 byla kvalitní, mělo by nalezení kolizí narozeninovým paradoxem vyžadovat cca 2⁸⁰ operací. Množství operací 2⁶⁹ je stále ještě vysoké a mnoho lidí bude obhajovat velkou náročnost prolomení. Budou mít pravdu, ale z kryptografického hlediska a z hlediska perspektivních nástrojů SHA-1 již bohužel skončila. Viz též stanovisko NIST dále. Kromě toho se pravděpodobně podaří složitost nalezení kolize v praxi snížit na 2⁶⁶.

8. Některé aplikace, využívající kolize hašovacích funkcí

8.1. Příklady využití již publikované čínské kolize MD5

V prosinci 2004 byly publikovány dva příklady ([OM2004], [DK2004]), jak lze využít nikoli schopnost generovat kolize, ale pouhou jednu jedinou datovou kolizi MD5, známou v té době, ke konstrukci sofistikovaných útoků. Zejména v práci [OM2004] jsou ukázány velké možnosti. Podle ní lze v konečném důsledku určitým postupem docílit toho, že libovolné dva různé, útočníkem volené soubory, se uživatelům jeví jako naprosto shodné, a to prostřednictvím kontroly haše a digitálního podpisu.

8.2. Jak oklamat certifikační autoritu, používající MD5 nebo SHA-1, aby vydala certifikát na dva různé podpisové klíče

V [LWW05a] z 1.3. 2005 je ukázán příklad podvržení jiného obsahu do již podepsaného a vydaného certifikátu. Využívá se možnost nalezení kolize MD5 pro zvolenou inicializační hodnotu. To umožní konstruovat zprávy s libovolným začátkem (zarovnaným na 64 bajtů) doplněných odlišnými bloky (128 bajtů) a pokračujícími libovolným dalším stejným obsahem. Oněch odlišných 64 bajtů se situuje do místa v certifikátu, kde je veřejný klíč (modul RSA), který je jádrem certifikátu, a který potvrzuje certifikační autorita svým digitálním podpisem v certifikátu. Výsledkem je, že útočník si může připravit dva různé klíče, na které bude mít vydaný jeden platný certifikát.

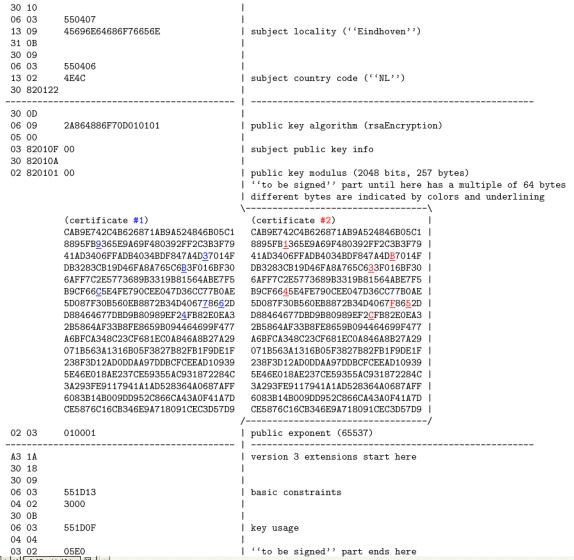
Tým Lenstra-Wang-Weger připravuje v těchto dnech spuštění experimentu na nalezení kolize certifikátu [LWW05b] podobně jako v [LWW05a], tentokrát ale pro hašovací funkci SHA-1. To už je velmi závažné, protože většina certifikačních autorit tuto funkci používá, a to jako silnější alternativu k MD5. Scénář je stejný jako u kolidujícího certifikátu MD5. Připraví se dva klíče, vypočte se inicializační hodnota pro kolizi SHA-1, prof. Wangová poskytne kolizi a zbytek je stejný jako předtím. Zbývá generovat kolizi SHA-1. Před měsícem oznámená složitost 2⁶⁹ se ale pravděpodobně podaří snížit na 2⁶⁶. Pracuje se již jen na získání výpočetního výkonu.

9. Klíčovaný hašový autentizační kód - HMAC

Klíčované hašové autentizační kódy zpráv HMAC zpracovávají hašováním nejen zprávu M, ale spolu s ní i nějaký tajný klíč K. Jsou proto podobné autentizačnímu kódu zprávy MAC, ale místo blokové šifry využívají hašovací funkci. Používají se jak k nepadělatelnému zabezpečení zpráv, tak k autentizaci (prokazováním znalosti tajného klíče K). Klíčovaný hašový autentizační kód je obecná konstrukce, která využívá obecnou hašovací funkci. Podle toho, jakou hašovací funkci používá konkrétně, označuje se výsledek, například HMAC-SHA-1(M, K) používá SHA-1, M je zpráva a K je tajný klíč.

9.1. Obecná definice HMAC

HMAC je definován ve standardu FIPS PUB 198 [32], kde je o něco obecněji popsán, než v RFC 2104 a ANSI X9.71. Jeho definice závisí na tom, kolik bajtů (B) má blok kompresní funkce. Například u SHA-1 je B = 64, u SHA- 384 a SHA-512 je B = 128.

Definujeme konstantní řetězce ipad jako řetězec B bajtů s hodnotou 0x36 a opad jako řetězec B bajtů s hodnotou 0x5C. Klíč K doplníme bajty 0x00 do délky B a definujeme hodnotu HMAC jako

HMAC-H(M, K) = H( (K xor opad) || H((K xor ipad)|| M) ),

kde || označuje zřetězení. Kolize HMAC nejsou kolizemi použité funkce ohroženy, neboť dnes se neumí nalézt kolize pro utajenou inicializační hodnotu. Situaci znázorňuje obrázek.

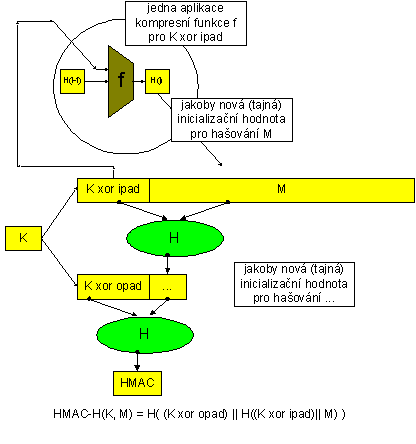
Obr.: Klíčovaný hašový autentizační kód zprávy HMAC-H(K, M)

Klíčovaný hašový autentizační kód zprávy HMAC-H(K, M) je funkčně podobný autentizačnímu kódu zprávy MAC, ale místo blokové šifry využívá hašovací funkci (H). Označuje se konkrétně podle toho, jakou hašovací funkci používá, např. HMAC-SHA-1(K, M). M označuje zprávu a K klíč. Je definován ve standardu FIPS 198 (kde je popsán o něco obecněji než v RFC 2104 a ANSI X9.71) a jeho definice závisí na délce bloku kompresní funkce v bajtech (např. u MD5/SHA-1/SHA-256 je to B = 64 bajtů, u SHA-384/SHA-512 je to B = 128 bajtů) a na délce hašového kódu hašovací funkce H. HMAC používá dvě konstanty, a to ipad jako řetězec B bajtů s hodnotou 0x36 a opad jako řetězec B bajtů s hodnotou 0x5C. Klíč K se doplní nulovými bajty do plného bloku délky B a poté definujeme

HMAC-H(K, M) = H( (K xor opad) || H((K xor ipad)|| M) ), kde || označuje zřetězení. Na obrázku je schéma HMAC.

Tajný klíč se modifikuje konstantou ipad a výsledek (K xor ipad) tvoří začátek vstupu do hašování. Je to definováno tak, že K xor ipad je přesně jeden blok kompresní funkce, takže po jeho zpracování dostáváme kontext H₁. Následuje zpracování zprávy M, čili její hašování jakoby začínalo z (útočníkovi neznámé) inicializační hodnoty IV = H₁, bez uvažování předsazeného řetězce (K xor ipad). Tento princip se použije ještě jednou, ale nikoli na zprávu jako takovou, nýbrž na obdrženou haš. Uvědomme si, že stačí nalézt jen kolizi pro H((K xor ipad)|| M), protože ta se automaticky projeví v celém HMAC.

Po publikování [WY2005] víme, že se tato práce nijak netýká kolize pro tajné nastavení inicializační konstanty, proto konstrukci HMAC považujeme za nedotčenou současnými útoky. Avšak odhaduje se, že i při tajné inicializační hodnotě by nalezení kolize mohlo být výpočetně méně náročné než by mělo teoreticky mělo být.

Proti použití prolomených hašovacích funkcí ve funkci HMAC v současné době není námitek, neboť není známo žádné oslabení funkce autentizačního kódu. Je však nutné sledovat, zda se útok neprohloubí i na tajné inicializační hodnoty.

9.2. Nepadělatelný integritní kód, autentizace původu dat

Zabezpečovací kód HMAC-SHA-1(M, K), pokud je připojen za zprávu M, detekuje neúmyslnou chybu při jejím přenosu. Případnému útočníkovi také zabraňuje změnit zprávu a současně změnit HMAC, protože bez znalosti klíče K nelze nový HMAC vypočítat. HMAC může být proto chápán jako nepadělatelný integritní kód, který samotná haš neposkytuje. Pro komunikujícího partnera je správný HMAC také autentizací původu dat, protože odesílatel musel znát hodnotu tajného klíče K.

9.3. Průkaz znalosti při autentizaci entit

HMAC může být použit jako průkaz znalosti tajného sdíleného tajemství (K) při autentizaci entit. Princip průkazu je tento. Dotazovatel odešle nějakou náhodnou výzvu (řetězec) challenge a od prokazovatele obdrží odpověď response = HMAC(challenge, K). Nyní ví, že prokazovatel zná hodnotu tajného klíče K. Přitom případný útočník na komunikačním kanálu z hodnoty response klíč K nemůže odvodit.

10. PRF a PRNG a odhad jejich oslabení současnou kryptoanalýzou

I když z teoretického hlediska nejsou hašovací funkce náhodná orákula, prakticky se tak jeví. Každá změna byť i jednoho bitu na vstupu má za následek nepredikovatelnou náhodnou změnu všech bitů na výstupu s pravděpodobností 1/2. A naopak jakákoliv změna na výstupu by měla vést k nepredikovatelné a náhodné změně na vstupu. Náhodnosti a nepredikovatelnosti se začalo využívat v různých technikách, a to i ve spojení s tajným klíčem. Jedná se o pseudonáhodné funkce PRF a pseudonáhodné generátory PRNG.

10.1. Pseudonáhodná funkce (PRF) při tvorbě klíčů z passwordů (PKCS#5)

Standard PKCS#5 umožňuje využít hašovací funkci k tvorbě "náhodného" šifrovacího klíče z passwordu pomocí pseudonáhodné funkce PRF jako klíč = PRF(password). Předpis je vidět z obrázku a vynecháme-li hodnotu soli, spočívá v hašování passwordu a následném mnohonásobném hašování výsledku. Počet hašování je dán konstantou c, jejíž hodnota se doporučuje minimálně 1000, ale používá se i 2000.

Výsledkem je krátký "náhodně vyhlížející" klíč DK, který je možné využít lépe než původní password. Jednak má pevnou délku a jednak z něho lze využít tolik bitů, kolik potřebujeme. Hodnota DK má pochopitelně lepší statistické vlastnosti než původní password. Tento postup se využívá ke tvorbě krátkých klíčů.

Obr.: Tvorba klíče DK z passwordu P podle PKCS#5 (S je sůl)

Zde nalézání kolizí čínskou metodou nevadí, i když je to "vada na kráse", protože bychom rádi, aby použitá hašovací funkce byla co nejkvalitnější ze všech hledisek.

10.2. Pseudonáhodné generátory (PRNG)

Typické použití hašovacích funkcí jako pseudonáhodných funkcí je v případech, kdy máme k dispozici krátký řetězec dat (seed) s dostatečnou entropií. Může se jednat například o "krátký" 256bitový náhodný šifrovací klíč, záznam náhodného pohybu myši na displeji, časový profil náhodných stisků kláves apod. Přitom potřebujeme z tohoto vzorku získat pseudonáhodnou posloupnost o velké délce, například 1 GByte apod. A k promítnutí entropie původního vzorku (seedu) do delší posloupnosti se právě používají hašovací funkce.

Hlavní rozdíl oproti minulému použití je v tom, že vstupem je náhodný zdroj, a další rozdíl je, že výstupem je dlouhá posloupnost.

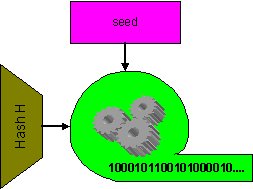
Obr.: Hašovací funkce v konstrukci PRNG

Tím, že je vstupem náhodný (útočníkovi neznámý) řetězec, dostáváme se s využitím kolizí do podobné situace jako u HMAC, protože útočník nezná inicializační hodnotu. Navíc jsou zde další složitosti. Uvedeme si příklady.

10.3. PRNG ve spojení s hašovací funkcí H, PKCS#1 v.2.1

Například standard PKCS#1 v.2.1 definuje pseudonáhodný generátor MGF1 (Mask Generation Function) pomocí hašovací funkce H s počátečním - většinou náhodným - nastavením seed takto:

H(seed || 0x00000000), H(seed || 0x00000001), H(seed || 0x00000002), H(seed || 0x00000003), ....

Protože seed je náhodný, konstrukce bude pravděpodobně bezpečná a současnými útoky nedotčená.

10.4. PRNG ve spojení s hašovací funkcí podle PKCS#5

Tam, kde seed není zcela náhodný, se používá komplikovanější postup, viz například funkce PBKDF2(P, S, c, dklen) z PKCS#5. Ta na základě passwordu P a soli S generuje pseudonáhodnou posloupnost (c je konstanta - hodnota čítače, např. 1000 nebo 2000):

T₁, T₂, T₃, ..., kde T_i, je vždy součet (xor) sloupce v následující tabulce. Počet řádků v tabulce odpovídá počtu (c) iterací.

U1 = H(P, S, 0x00000001)	U1 = H(P, S, 0x00000002)		U1 = H(P, S, i (4Byte))
U2 = H(P, U1)	U2 = H(P, U1)		U2 = H(P, U1)
U3 = H(P, U2)	U3 = H(P, U2)		U3 = H(P, U2)
U4 = H(P, U3)	U4 = H(P, U3)		U4 = H(P, U3)
....	....	....	....
Uc = H(P, Uc-1)	Uc = H(P, Uc-1)		Uc = H(P, Uc-1)
T1 = součet (xor) sloupce	T2 = součet (xor) sloupce		Ti = součet (xor) sloupce

Tab.: Pseudonáhodný generátor PBKDF2(P, S, c, dklen) podle PKCS#5

Protože tato konstrukce je velmi robustní, není tu vůbec zřejmé, jak by se mohla schopnost nalézání kolizí projevit na bezpečnostních vlastnostech těchto konstrukcí. Pochopitelně, pokud by hašovací funkce byla velmi primitivní (například kód CRC), i tyto konstrukce by byly ohroženy. Současné hašovací funkce ale velmi primitivní rozhodně nejsou, ani u nich nejsou známy takové uvedené slabiny

Obecně můžeme opět říci, že není znám žádný útok na PRNG ve spojení s prolomenými hašovacími funkcemi. Je samozřejmě lepší je nahradit za kvalitní, pokud to lze.

Poznamenejme, že dodatek o obezřetnosti platí pro všechny hašovací funkce (viz úvod - není prokázána jejich "bezpečnost", jak bychom si představovali), takže je jenom větším zdůrazněním obecné vlastnosti v tomto konkrétním případě, kde by nějaká nežádoucí slabina mohla eventuelně vzniknout.

10.5. PRNG ve spojení s HMAC

Poznamenejme, že namísto H v předchozích nebo jiných PRNG je možné použít HMAC. Taková konstrukce je ještě robustnější než PRNG ve spojení s H, proto ani u PRNG ve spojení s HMAC zde nejsou známy žádné negativní důsledky čínského útoku.

11. Kolize a některá autentizační schémata

Existují i různé příklady využívající dokonce digitální podpisy, kde slabší odolnost proti kolizi tolik nevadí. Jedná se většinou o autentizační schémata. Můžeme si uvést následující primitivní příklad autentizace, kdy ten, kdo autentizuje (řekněme nějaká webová aplikace), vyšle náhodnou výzvu RND uživateli. Ten aplikaci vrátí digitálně podepsanou hašovací hodnotu h(RND). Tím se autentizuje, neboť aplikace si jeho podpis může ověřit. V tomto případě nalézání kolizí útočníkovi nepomůže, protože výzvu RND nevytváří on, ale aplikace. I kdyby útočník dokonce uměl nalézt kolizi 2. řádu, tj. nalézt RND´ tak, že h(RND) = h(RND´), nemůže se za uživatele přihlásit.

12. Třída hašovacích funkcí SHA-2 (SHA-256, 384, 512 a 224)

Z důvodu zvýšení odolnosti vůči kolizím je od 1. února 2003 k dispozici nová trojice hašovacích funkcí SHA-256, SHA-384 a SHA-512 [SHA-2] a od února 2004 SHA-224 (dodatek [SHA-2]). Tyto funkce přichází se zvýšením délky hašového kódu na 256, 384 a 512 bitů (SHA-224 má 224 bitový hašový kód), což odpovídá složitosti 2¹²⁸, 2¹⁹² a 2²⁵⁶ pro nalezení kolizí narozeninovým paradoxem. To je jednak už dost vysoká složitost a také to odpovídá složitosti útoku hrubou silou na tři délky klíčů, které nabízí standard AES.

Pokud se týká konstrukce nových funkcí, jsou velmi podobné SHA-1 a používají stejné principy, pracují však se složitějšími funkcemi a širšími vstupy. Podrobnosti lze nalézt v uvedených standardech. Jejich cílem bylo poskytnout větší odolnost proti kolizi a nabídnout odpovídající bezpečnost jako klíče pro AES.

13. Generické problémy iterativních hašovacích funkcí

Generické problémy hašovacích funkcí ukazují dvě práce. První představil Joux [Joux04] na konferenci Crypto v srpnu 2004 a druhý Kelsey-Schneier [KS2004] v listopadu 2004. Obě dvě práce ukazují, že iterativní konstrukce hašovací funkce implikuje značnou odlišnost této funkce od náhodného orákula.

Joux ukazuje, že

1) u iterativních hašovacích funkcí lze docílit mnohonásobné kolize mnohem jednodušeji než ve srovnání s náhodným orákulem

2) kaskádovitá konstrukce F || G pomocí dvou hašovacích funkcí pozbývá smyslu, neboť očekávaná složitost nalezení kolize není součinem dílčích složitostí, ale spíše součtem

Kelsey-Schneierova práce

1) obsahuje výrazně zlepšenou metodu konstrukce multikolizí oproti Jouxovi,

2) umožňuje konstruovat druhý vzor zprávy u iterativních hašovacích funkcí se složitostí cca 2*2^n/2 + 2^n-k+1 pro velmi dlouhé zprávy o délce 2^k blízké 2^n/2_.

Konkrétně pro SHA1 lze ke zprávě o délce 2⁶⁰ bajtů vytvořit druhý vzor se složitostí 2¹⁰⁶ na rozdíl od teoretické složitosti 2¹⁶⁰.

13.1. r-násobná kolize pro iterativní hašovací funkce lze docílit s nižší složitostí

Joux [Joux04b] ukázal, že u iterativních hašovacích funkcí lze r-násobnou kolizi najít se složitostí ln₂r * 2^n/2 namísto 2^{n*(r - 1) /r}.

Postup. Vyjdeme ze standardní hodnoty IV, H₀ = IV, se složitostí S(F) najdeme kolizi hašovací funkce F s inicializační hodnotou H₀ (zprávy M_1,1 a M_1,2). Výslednou haš označme H₁. Se složitostí S(F) nalezneme kolizi F s inicializační hodnotou H₁ (zprávy M_2,1 a M_2,2), výslednou haš označíme H₂. Takto uděláme N kroků pro N = ln₂r. Nyní můžeme sestavit 2^N = r zpráv, majících tutéž haš H_N, a to tak, že z každé dvojice bloků M_i,1 a M_i,2 vybereme vždy jednu z nich. Dostaneme tak 2^N zpráv, které prochází stejnými hašovacími mezivýsledky a končí stejným hašovacím kódem H_N.

13.2. Kaskádovitá konstrukce pozbývá smyslu

Druhou vlastností, kterou Joux [Joux04b] odhalil, je že složení hašovacích funkcí F a G (kaskáda), F||G (|| označuje zřetězení) neposkytuje intuitivně předpokládanou bezpečnost, ale mnohem nižší. Předpokládalo se, že složitost S(F||G) nalezení kolize hašovacího kódu F(x)||G(x) bude rovna součinu složitostí nalezení kolizí dílčích hašovacích kódů, tj. S(F||G) = S(F) * S(G). Joux ukázal, že je to jen o něco více než S(F) + S(G), přičemž postačí, aby pouze F byla iterativní hašovací funkce, zatímco G může být i náhodné orákulum. Stručně řečeno kaskádovitá konstrukce pozbývá smyslu, protože výsledný kód je přibližně pouze tak složitý jako silnější z dílčích hašovacích funkcí. Tyto dvě vlastnosti přímo neohrožují žádné prakticky používané schéma, ale ukazují, že iterativní konstrukce není ideální, neboť oddaluje takové hašovací funkce od náhodného orákula.

Postup.

• Nechť F je iterativní hašovací funkce s délkou hašovacího kódu n_f £ n_g.
• Potom se složitostí n_g/2 * S(F) vytvoříme n_g/2 návazných kolizí funkce F, které dávají 2^ng/2 - násobnou multikolizi vzhledem k F.
• Mezi těmito 2^ng/2 zprávami nalezneme jednu kolizi vzhledem ke G.
• Máme tedy dvě zprávy, které mají stejný hašový kód vzhledem k F i G, tj. k F||G.

Složitost je n_g/2 * S(F) + 2^ng/2 (druhý sčítanec je počet hašování G), tedy n_g/2 * S(F) + S(G) » S(F) + S(G).

Intuitivně se očekávalo, že složením kvalitní hašovací funkce F o délce kódu n_f a funkce G o délce kódu n_g vznikne kvalitní hašovací funkce o délce kódu n_f + n_g a složitosti nalezení kolize bude 2^(nf+ng)/2. Místo toho je to mnohem méně, n_g/2 * 2^nf/2 + 2^ng/2.

13.3. Nalezení druhého vzoru u dlouhých zpráv snadněji než se složitostí 2ⁿ

V práci [KS2004] se tato vlastnost ukazuje pro dlouhé zprávy, o délce blízké 2^n/2 bloků. Postup (zkrácený postup s využitím pevných bodů).

· Nechť zpráva M má délku 2^k bloků.

· Vytvoříme seznam průběžných kontextů K_t při hašování zprávy M = m₁, m₂ ,..., m_t, .... Je jich 2^k.

· Volíme náhodně 2^n/2 bloků M_i , které dávají seznam 2^n/2 haší h_i = h(H₀, M_i).

• Volíme náhodně 2^n/2 bloků N_j a z N_j určíme pevný bod H_j = f(H_j , N_j), využijeme k tomu Davies-Meyerovy konstrukce.
• Nalezneme kolizi mezi seznamy {H_j} a {h_i}, tj. i* a j* tak, že h_i* = H_j* .

· Volíme náhodně 2^{n - k} bloků Mlink_l , které dávají seznam 2^{n - k} haší hlink_l = h(H_j*, Mlink_l).

• Nalezneme kolizi mezi seznamy {hlink_l} a {K_t}, tj. l* a t* tak, že hlink_l* = K_t* .

· Zpráva (M_i*, N_j*, Mlink_l*) a prvních i bloků zprávy M dávají stejný hašovací kontext K_t* .

• Tyto zprávy mají různou délku, ale zprávu (M_i*, N_j*, Mlink_l*) doplníme o potřebný počet bloků na délku i bloků jako (M_i*, N_j*, N_j*,..., N_j*, Mlink_l*). Za obě zprávy pak připojíme zbytek zprávy M a dostaneme druhý vzor zprávy M.

Složitost je 2^n/2 (seznam M_i) + 2^n/2 (seznam N_j) + 2^n-k (seznam Mlink_l) + 2^k (seznam K_t) = 2^n/2+1 + 2^n-k + 2^k » 2^n/2+1 + 2^n-k+1_. To je mnohem méně než 2ⁿ.

13.4. Závěr k novým zjištěním kryptoanalýzy iterativních hašovacích funkcí.

Řada předních kryptologů se shoduje v tom, že je nutno zahájí práce na veřejné mezinárodní soutěži na nový koncept hašovacích funkcí, neboť iterativní funkce nesplňují požadované bezpečnostní vlastnosti.

Uvedené odhalené vlastnosti jsou teoretického rázu, ale jednoho dne by se mohly projevit zcela prakticky. Proto je nezbytná změna konceptu.

14. NIST plánuje přechod na SHA-2 do r. 2010

Americký standardizační úřad NIST, který za standardy hašovacích funkcí odpovídá, vydal 25. 8. 2004 prohlášení k tehdejším současným výsledkům na [NIST05a], z něhož vyjímáme:

• Doporučuje se používat třídu funkcí SHA-2.
• Do roku 2010 se předpokládá opuštění i SHA-1 a přechod na SHA-2.

Po oznámení možnosti nalézt kolizi SHA-1 za 2⁶⁹ operací NIST 23. 2. 2005 potvrdil svoje dřívější stanovisko [NIST05b].

15. Závěr: Které techniky jsou a nejsou bezpečné

• Prolomené hašovací funkce by se neměly používat tam, kde se jedná o nepopiratelnost, tedy u digitálních podpisů.
• Klíčované hašové autentizační kódy zpráv HMAC ani pseudonáhodné funkce PRF a pseudonáhodné generátory PRNG, které používají hašovací funkce jako nástroje, zatím nejsou současnou kryptoanalýzou dotčeny.
• Je tu ale možné riziko pramenící z toho, že máme jen velmi málo informací o technikách prolomení současných hašovacích funkcí a že lze v této oblasti očekávat pokrok. To je hrozba, kterou si každý musí ohodnotit.
• Dále víme, že iterativní konstrukce hašovací funkce vede k rozporu s vlastnostmi náhodného orákula. To může časem také přinést nová odhalení vlivu této konstrukce na kvalitu PRNG s těmito hašovacími funkcemi.

15.1. Doporučení

• Je vhodné provést revizi všech aplikací, kde jsou použity hašovací funkce MD4, MD5, SHA-0, RIPEMD a HAVAL-128.
• Je-li některá z těchto funkcí použita pro účely digitálních podpisů (s klasickým účelem zajištění nepopiratelnosti), je nutno tuto funkci nahradit.
• U funkce SHA-1 je nutné ji nahradit nebo zvážit riziko jejího ponechání v každé aplikaci. Jde zejména o možnost vzniku škody "zpětně", tj. argumentací v budoucnu, kdy by byla SHA-1 prolomena, že mohla být prolomena již teď, tj. v minulosti.
• Podle okolností provést náhradu za některou z funkcí SHA-2, které jsou zatím považovány za bezpečné (SHA-256, SHA-384 nebo SHA-512, nejlépe SHA-512 [SHA-1,2]).
• U funkce SHA-1 zahájit nebo naplánovat v brzké době její výměnu za některou z funkcí z třídy SHA-2. Není-li to možné, zvážit riziko jejího dalšího používání.
• Je-li některá z uvedených těchto funkcí použita pro účely HMAC nebo PRNG, individuálně posoudit, zda je toto užití bezpečné nebo ne.

16. Literatura

[ARCHIV] Archiv autora obsahující články o kryptologii a bezpečnosti, http://cryptography.hyperlink.cz/

[BC04a] Biham, Eli, Chen, Rafi: Near Collisions of SHA-0, CRYPTO 2004

http://www.cs.technion.ac.il/users/wwwb/cgi-bin/tr-get.cgi/2004/CS/CS-2004-09.ps.gz

[BC04b] Eli Biham, Rafi Chen: New results on SHA-0 and SHA-1, CRYPTO 2004 Rump Session

[BoBo93] B. den Boer and A. Bosselaers. Collisions for the compression function of MD5. In Advances in Cryptology, Eurocrypt ‘93, pages 293-304, Springer-Verlag, 1994.

[D96a] H. Dobbertin, Cryptanalysis of MD4, Fast Software Encryption 1996, LNCS, Vol. 1039, Springer-Verlag, 1996, pp. 53 - 69

[DK2004] Dan Kaminsky: MD5 To Be Considered Harmful Someday, Cryptology ePrint Archive, Report 2004/357, http://eprint.iacr.org/2004/357, 6 December 2004

[DO96eu] H. Dobbertin. Cryptanalysis of MD5 Compress. Presented at the rump session of Eurocrypt ‘96, May 14, 1996.

[DO96cb] H. Dobbertin. The Status of MD5 after a Recent Attack. CryptoBytes, 2(2): 1-6, 1996.

[HAVAL] Y. Zheng, J. Pieprzyk, J. Seberry, HAVAL - A One-way Hashing Algorithm with Variable Length of Output, Auscrypt 92

[HMAC] FIPS PUB 198, The Keyed-Hash Message Authentication Code (HMAC), NIST, US Department of Commerce, Washington D. C., March 6, 2002, http://csrc.nist.gov/CryptoToolkit/tkhash.html, resp. RFC 2104, http://www.rfc-editor.org/

[HPR04] Philip Hawkes, Michael Paddon, Gregory G. Rose: Musings on the Wang et al. MD5 Collision, Cryptology ePrint Archive, Report 2004/264, 13 October 2004, http://eprint.iacr.org/2004/264.pdf

[Joux04a] Antoine Joux: Collisions in SHA-0, CRYPTO 2004 Rump Session

[Joux04b] A. Joux: Multicollisions in iterated hash functions. Application to cascaded

constructions. Proceedings of Crypto 2004, LNCS 3152, pages 306-316.

[KS2004] John Kelsey, Bruce Schneier: Second Preimages on n-bit Hash Functions for Much Less than 2^n Work, http://eprint.iacr.org/2004/304/, November 15, 2004

[LWW05a] Arjen Lenstra, Xiaoyun Wang and Benne de Weger: Colliding X.509 Certificates, Cryptology ePrint Archive, Report 2005/067, http://eprint.iacr.org/2005/067

[LWW05b] Arjen Lenstra, Xiaoyun Wang and Benne de Weger: Colliding X.509 Certificates based on SHA1-collisions, http://www.win.tue.nl/~bdeweger/CollidingCertificates/index.html

[MD245] MD2, MD4, MD5 - RFC 1319, 1320, 1321, http://www.rfc-editor.org/

[NIST05b] NIST Brief Comments on Recent Cryptanalytic Attacks on SHA-1

http://csrc.nist.gov/news-highlights/NIST-Brief-Comments-on-SHA1-attack.pdf

[NIST05a] NIST Brief Comments on Recent Cryptanalytic Attacks on Secure Hashing Functions and the Continued Security Provided by SHA-1, http://csrc.ncsl.nist.gov/hash_standards_comments.pdf,

[OOW94] P. van Oorschot and M. Wiener. Parallel collision search with application to hash functions and discrete logarithms. In Proceedings of 2nd ACM Conference on Computer

and Communication Security, pages 210-218, ACM Press, 1994.

[OM2004] Ondrej Mikle: Practical Attacks on Digital Signatures Using MD5 Message Digest, Cryptology ePrint Archive, Report 2004/356, http://eprint.iacr.org/2004/356, 2nd December 2004, http://cryptography.hyperlink.cz/2004/collisions.htm

[PKCS2] PKCS#5 v2.0: Password-Based Cryptography Standard, RSA Labs, March 25, 1999

[RIPEMD-160] H. Dobbertin, A. Bosselaers, B. Preneel, "RIPEMD-160: A Strengthened Version of RIPEMD," Fast Software Encryption, LNCS 1039, D.Gollmann, Ed., Springer-Verlag, 1996, pp. 71-82

[SHA-0] FIPS 180 (superseded by FIPS 180-1 and FIPS 180-2), Secure hash standard (SHS), NIST, US Department of Commerce, Washington D. C., May 1993

[SHA-1] FIPS 180-1 (superseded by FIPS 180-2), Secure hash standard (SHS), NIST, US Department of Commerce, Washington D. C., April 1995

[SHA-2] FIPS 180-2, Secure Hash Standard (SHS), NIST, US Department of Commerce, Washington D. C., August 2002 (change notice: February 2004), http://csrc.nist.gov/publications/fips/fips180-2/fips180-2withchangenotice.pdf, platný standard, obsahuje definice SHA-1, SHA-224, SHA-256, SHA-384 a SHA-512

[VK2005] Vlastimil Klima: Finding MD5 Collisions – a Toy For a Notebook, Cryptology ePrint Archive, Report 2005/075, http://eprint.iacr.org/2005/075, (v češtině " Nalézání kolizí MD5 - hračka pro notebook", http://cryptography.hyperlink.cz/md5/MD5_kolize.pdf.)

[WFLY04] X. Wang, D. Feng, X. Lai, H. Yu, "Collisions for Hash Functions MD4, MD5, HAVAL-128 and RIPEMD", rump session, CRYPTO 2004, Cryptology ePrint Archive, Report 2004/199, http://eprint.iacr.org/2004/199

[WY2005] Xiaoyun Wang and Hongbo Yu: How to Break MD5 and Other Hash Functions, http://www.infosec.sdu.edu.cn/paper/md5-attack.pdf.

[WYY05] Wang X., Yin L., Yu H.: Collision Search Attacks on SHA1, February 13, 2005, http://theory.lcs.mit.edu/~yiqun/shanote.pdf